Geometry

GEOMETRY
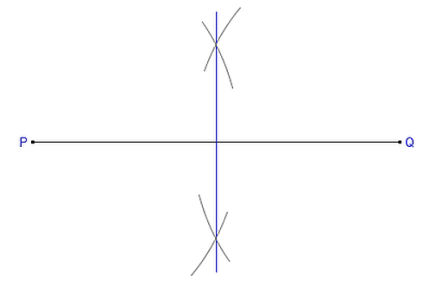
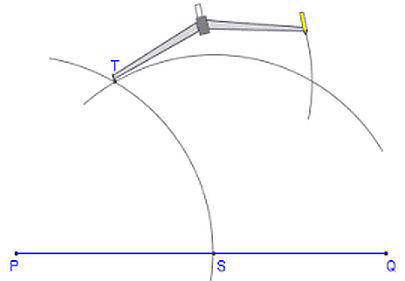
I've been tossing around terms like; erect a perpendicular, strike an arc; geometry.
Unlike what you may have thought
in Middle School; Geometry is your friend.

The most frequently used method for erecting a perpendicular
is by reference to a precise copy of a right angle - Framing/Rafter, Speed, Combination, Try, Drywall, Miter, (the Sliding Bevel)
and the Stanley 46-101 Center Square.
The 3,4,5 right triangle and comparing diagonals? Definite force
multipliers. However, all (except the Try, Miter and Sliding Bevel squares)
involve measurement.

There is another family of techniques -
the “straightedge and compass constructions.”
Very useful; and often involve no measurement or calculation at all.
There's a nice compilation at mathopenref.com
with nifty animations and clear explanations.

These are the ones I used most often.
Simplest first.
Bisect a line.
Perpendicular to a line from a point
Erecting a perpendicular from a line
at a stated point
Parallel

[Quick and dirty method for paralell
(4+ tangents - Euclid would not approve; but he might wink.)
When striking an arc you can feel the scribing end move away from and back towards you. If you know the distance from the baseline to the parallel; set your compass to that distance and strike 4-5 arcs from along the baseline; where you feel both the push and the pull. A straight line that kisses the extreme extents of all of those arcs (NOT THE POINTS WHERE THEY MAY, BY HAPPENSTANCE, INTERSECT) is parallel to the baseline at the stated distance.]

A Perpendicular gives you 90 degrees.
You can also construct 60 and 30 degree angles

You can bisect an angle, very useful if you have to start from a given (and not a stated) angle

You can add or subtract angles from one another
to derive a whole assortment of useful angles.

Also useful to remember:
Finding the center of a circle or an arc.

The perpendicular bisector of a chord
lies along the radius of that arc.
The point at which two or more of such radius lines (radii)
intersect is the center of that arc.
The center head on a combination square or the 46-101 Center Square both operate via the principle of the perpendicular bisector of a chord.

The points at which the two limbs of any right angle (rafter square e.g.) placed against an arc both intersect that arc, describes a diameter of that arc. The point at which two diameters intersect one another is the center of that arc.

USPS

eMail

Links